들어가기 전에...
해당 글은 유데미 JavaScript 알고리즘 & 자료구조 마스터클래스 강의를 바탕으로 더 효율적이고 간결하게 수정된 코드이다.
✅ 그래프란?
유한하고 변할 수 있는 꼭지점이나 노드나 점들의 집합으로 구성된 데이터 구조
💡 구성 요소
- 정점(vertax): 각 노드
- 간선(edge): 정점을 잇는 선
💡 그래프의 종류
- 트리: 두 개의 정점이 하나의 경로로 이어져 있는 그래프
- 유방향/무방향 그래프: 간선의 방향 유무로 구별되는 그래프
- 가중/비가중 그래프: 간선에 값 부여 여부로 구별되는 그래프
- 밀집 그래프: 노드 ↓, 간선 ↑ / 희소 그래프: 노드 ↑, 간선 ↓
ex) 구글 맵을 만든다면 => 가중 & 유방향 그래프
(가중 - 위치 사이에 거리가 값으로 부여 / 유방향 - 일방통행, 쌍방통행 거리로 나눠짐)
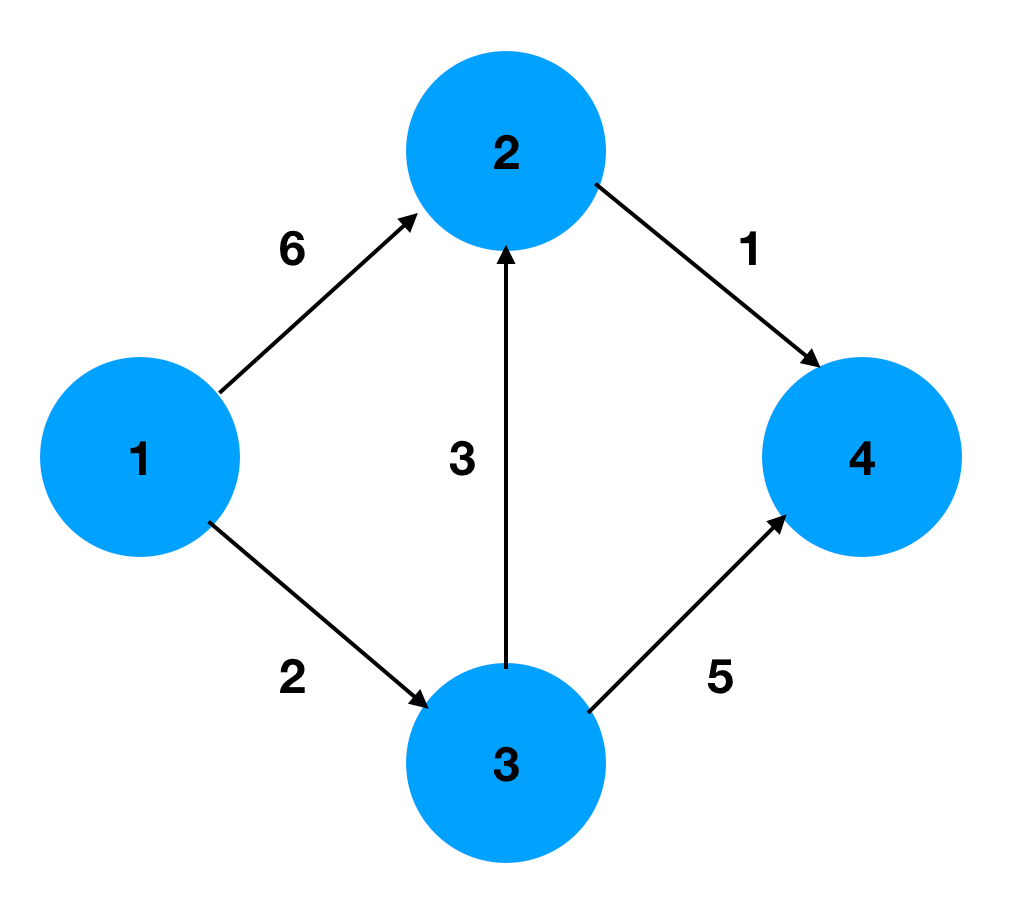
📌 구현 방법 - 인접 리스트 vs 인접 행렬
인접 행렬
인접 리스트
출처: 제로초 블로그
💡 시간복잡도
- V : 정점 개수
- E : 간선 개수
| 인접 리스트 | 인접 행렬 | |
|---|---|---|
| 정점 추가 | O(1) | O(V^2) |
| 간선 추가 | O(1) | O(1) |
| 정점 삭제 | O(V+E) | O(V^2) |
| 간선 삭제 | O(E) | O(1) |
| 검색 | O(V+E) | O(1) |
| 저장 | O(V+E) | O(V^2) |
💡 장단점
| 인접 리스트 | 인접 행렬 | |
|---|---|---|
| 메모리 차지 (in 희소 그래프) |
비교적 작음 (실제 연결된 간선만 저장) |
비교적 큼 (간선이 아니어도 0으로 저장됨) |
| 간선 순회 | 비교적 빠름 | 비교적 느림 |
| 특정 간선 검색 (연결 확인) |
비교적 느림 | 비교적 빠름 (행렬의 값만 확인하면 됨) |
📌 구현 (인접 리스트)
메모리를 덜 차지해서 효율적인 인접 리스트를 이용함
=> 인접 리스트는 해시 테이블로 구현
// 완성된 그래프 예시
const graph = {
"A": ["B", "C"],
"B": ["A", "D"],
"C": ["A", "E"],
"D": ["B", "E", "F"],
"E": ["C", "D", "F"],
"F": ["D", "E"]
}
class Graph {
constructor() {
this.adjacencyList = {};
}
// 정점 추가
addVertax(vertex) {
if(!this.adjacencyList[vertex]) this.adjacencyList[vertex] = [];
}
// 간선 추가
addEdge(v1, v2) {
this.adjacencyList[v1].push(v2)
this.adjacencyList[v2].push(v1)
}
// (가중그래프라면) 간선 추가
addEdge(v1, v2, weight) {
this.adjacencyList[v1].push({node: v2, weight});
this.adjacencyList[v2].push({node: v1, weight});
}
// 간선 제거
removeEdge(v1, v2) {
this.adjacencyList[v1] = this.adjacencyList[v1].filter(v => v !== v2);
this.adjacencyList[v2] = this.adjacencyList[v2].filter(v => v !== v1);
}
// 정점 제거
removeVertex(vertex) {
// 정점과 연결된 곳의 리스트에서 정점 삭제
this.adjacencyList[vertex].forEach(connectedV => {
this.adjacencyList[connectedV]
= this.adjacencyList[connectedV].filter(v => v !== vertex)
})
this.adjacencyList[vertex] = null; // 정점의 리스트 비움
delete this.adjacencyList[vertex]; // 완전히 삭제
}
}📌 순회
BFS (넓이 우선 순회)
function bfs(graph, startNode) {
let result = [];
let queue = [startNode];
let visited = {[startNode]: true};
let curVertex;
while(queue.length) {
curVertex = queue.shift();
result.push(curVertex);
graph[curVertex].forEach(neighbor => {
if(!visited[neighbor]) {
visited[neighbor] = true;
queue.push(neighbor);
}
})
}
return result;
}DFS (깊이 우선 순회)
// 1️⃣재귀적 용법
function depthFirstSearch(graph, startNode) {
let result = [];
let visited = {}; // 방문시 "A": true 같이 기록
(function dfs(vertex) {
if(!vertex) return; // 노드값이 올바르지 않을시 처리
result.push(vertex); // 결과값에 추가
visited[vertex] = true; // 방문 처리
graph[vertex].forEach(neighbor => { // 방문하지 않은 이웃 순회
if(!visited[neighbor]) dfs(neighbor);
})
})(startNode);
return result;
}
// 2️⃣반복적 용법
function dfs(graph, startNode) {
let result = [];
let stack = [startNode];
let visited = {[startNode]: true};
let curVertex;
while(stack.length) {
curVertex = stack.pop();
result.push(curVertex);
graph[curVertex].forEach(neighbor => {
if(!visited[neighbor]) {
visited[neighbor] = true; // 여기서 방문처리 했으니 이후 스택에 추가x
stack.push(neighbor);
}
})
}
return result;
}'Computer Science > Data structure' 카테고리의 다른 글
| [자료구조] 트라이(Trie) - javascript (0) | 2023.02.07 |
|---|---|
| [자료구조] 이진 힙 (Binary Heaps) - javascript (0) | 2023.01.24 |
| [자료구조] 이진 탐색 트리(Binary Search Tree) - javascript (0) | 2023.01.18 |
| [자료구조] 단일 & 이중 연결 리스트 - javascript (0) | 2023.01.18 |

