✅ 다익스트라 알고리즘이란?
가중 그래프에서 최적의 경로를 찾을 때 사용하는 알고리즘
- 다익스트라라는 네덜란드 프로그래머가 20분만에 카페에서 만듬
- GPS, 네트워크 라우팅 등 최적의 경로를 찾아야하는 경우에 많이 사용됨
💡 원리 및 실행과정
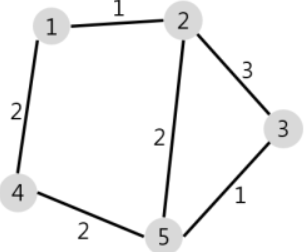
출발, 도착 노드를 설정 ex) 1
출발 노드부터 연결된 노드의 최소 거리 저장
ex) 1과 연결된 노드가 2, 4 이므로 두 노드에 최소 거리 저장 2(1), 4(2)
방문하지 않은 노드 중에서 가장 거리가 짧은 노드 선택
ex) 2(1), 4(2) 중 비용이 1로 적은 2 선택
선택한 노드와 연결된 노드의 최소 거리 저장 (저장한 값보다 작다면 최소로 갱신)
ex) 3(4), 5(3)
3,4번 반복 ⇒ 도착 노드를 뺀 모든 노드까지의 최소 경로 알 수 있음
도착 노드와 연결된 노드 중 최소 거리를 가진 것이 최적의 경로
💡 의사코드
- 출발, 도착 노드를 지정
- 필요한 자료구조 생성
- distance 객체: key - 노드 / value -노드까지의 최소 거리
- 초기값: 출발점 - 0 / 나머지 - infinity
- 우선순위 큐: 초기값은 빈 배열, 값은 {val: 노드명, priority: 노드까지의 최소 거리} 형태로 들어옴
- priority의 초기값: 출발점 - 0 / 나머지 - infinity
- previous 객체(경로 필요할 시) : key - 각 노드 / value: 현재 저장된 최소 거리의 경로에서 바로 전에 거쳐온 노드
- distance 객체: key - 노드 / value -노드까지의 최소 거리
- 우선순위 큐의 순서대로 노드 방문 순회
- 가장 우선순위가 높은 노드 꺼내서 방문
- 만약 현재 노드가 도착점이라면 끝
- 아니라면 현재 노드의 이웃 노드를 순회
- 현재 노드를 거쳐 이웃 노드로 가는 경로가 이웃 노드에 저장된 최소 거리보다 작음 → distances & previous 값 수정
- 3번 과정 반복
📌 필요한 자료구조
💡 가중 그래프
인접 리스트를 이용하여 구현함
class WeightedGraph {
constructor() {
this.adjacencyList = {};
}
// 정점 추가
addVertax(vertex) {
if (!this.adjacencyList[vertex]) this.adjacencyList[vertex] = [];
}
// 간선 추가
addEdge(v1, v2, weight) {
this.adjacencyList[v1].push({ node: v2, weight });
this.adjacencyList[v2].push({ node: v1, weight });
}
}
// 그래프 예시
{
A: [{node: 'B', weight: 4},
{node: 'C', weight: 2}],
B: [{node: 'A', weight: 4},
{node: 'D', weight: 1}],
C: ...
}💡 우선순위 큐
sort()를 이용한 방법 (간단하지만 비교적 느림)
class PriorityQueue { constructor() { this.values = []; } enqueue(val, priority) { this.values.push({ val, priority }); this.sort(); } dequeue() { return this.values.shift(); } sort() { this.values.sort((a, b) => a.priority - b.priority); } }최소 이진 힙을 이용한 방법 (비교적 빠름)
class PriorityQueue { constructor() { this.values = []; } // 노드 삽입 enqueue(val, priority) { this.values.push({val, priority}); if(this.values.length > 1) this.bubbleUp(newNode); return this.values; } bubbleUp(element) { let idx = this.values.length-1; let parentIdx, parentPriority; while(idx > 0) { parentIdx = Math.floor((idx-1)/2); parent = this.values[parentIdx]; if(parent.priority <= element.priority) break; [this.values[parentIdx], this.values[idx]] = [element, parent]; idx = parentIdx; } } // 루트 삭제 (우선순위 따져서 내보냄) dequeue() { if(this.values.length === 0) return false; let root = this.values[0]; let end = this.values.pop(); if(this.values.length > 0) { this.values[0] = end; this.sinkDown(); } return root; } sinkDown() { let element = this.values[0]; let priority = element.priority; let idx = 0; let lgth = this.values.length; while(true) { let leftChildIdx = idx * 2 + 1; let rightChildIdx = idx * 2 + 2; let leftChildPry, rightChildPry; let swap = null; if(leftChildIdx < lgth) { leftChildPry = this.values[leftChildIdx].priority; if(leftChildPry < priority) swap = leftChildIdx; } if(rightChildIdx < lgth) { rightChildPry = this.values[rightChildIdx].priority; if((swap === null && rightChildPry < priority) || (swap !== null && rightChildPry < leftChildPry)) swap = rightChildIdx; } if(swap === null) break; [this.values[swap], this.values[idx]] = [element, this.values[swap]]; idx = swap; } } }
📌 구현
아래 구현은 그래프와 우선순위 큐가 분리되어 있어
다른 함수에서도 재사용이 가능한 형태이다.
그러다보니 아래 함수는 원하는 값을 추출하고,
변수로 저장하고, 중복되는 부분이 있어 다소 복잡하다.
알고리즘 문제를 풀기 위해 해당 알고리즘을 사용한다면 이렇게 할 필요는 없다.
한 함수 안에서 그래프와 큐를 만들어서 다익스트라 알고리즘까지 적용하는
훨씬 간소화된 풀이는 아래에 따로 넣겠다!
function Dijkstra(graph, start, finish) {
const nodes = new PriorityQueue(); // 우선순위 큐
const distances = {};
const previous = {};
let smallest;
// 경로 필요하다면 생성
let path = [];
// nodes & distances & previous 초기값 세팅
for (let vertex in graph) {
if (vertex === start) {
// 시작점은 거리 0으로 세팅
distances[vertex] = 0;
nodes.enqueue(vertex, 0);
} else {
distances[vertex] = Infinity;
nodes.enqueue(vertex, Infinity); // 순회 중 노드가 누락될 수 있으니 먼저 다 넣음
}
previous[vertex] = null;
}
// 우선순위 큐가 빌 때까지 순회
while (nodes.values.length) {
smallest = nodes.dequeue().val;
// 만약 도착점이라면 종료 () 최소경로를 따라오던 중이었으니 종료하면 최소거리값이 도출됨
if (smallest === finish) {
return distances[smallest];
// 경로 필요하다면 아래까지 적기
while (smallest) {
path.push(smallest);
smallest = previous[smallest];
}
return path.reverse();
}
if (smallest || distances[smallest] !== Infinity) {
// 예외 처리 (안써도 됨, 거리 저장안됐을 때 처리)
graph[smallest].forEach((neighbor) => {
let neighborNode = neighbor.node;
let neighborEdge = neighbor.weight;
let newDistance = distances[smallest] + neighborEdge;
if (distances[neighborNode] > newDistance) {
distances[neighborNode] = newDistance; // 거리 최소값으로 갱신
previous[neighborNode] = smallest; // 이전 노드 갱신
nodes.enqueue(neighborNode, newDistance); // 우선순위 큐의 거리값 갱신 (추가하면 덮어쓰기->정렬됨)
}
});
}
}
}💡 알고리즘 문제풀이용 구현
function solution(graph, start, finish) {
let distances = {};
let queue = [];
function pushQueue(v) {
if (!queue.includes(v)) queue.push(v); // 중복 검사 후 추가
queue.sort((a, b) => distances[a] - distances[b]);
}
// 초기값 설정
for (let vertex in graph) {
if (vertex === start) distances[vertex] = 0;
else distances[vertex] = Infinity;
pushQueue(vertex);
}
while (queue.length) {
let smallest = queue.shift();
if (smallest === finish) return distances[smallest];
graph[smallest].forEach((neighbor) => {
let neighborNode = neighbor.node;
let newDistance = distances[smallest] + neighbor.weight;
if (distances[neighborNode] > newDistance) {
distances[neighborNode] = newDistance;
pushQueue(neighborNode);
}
});
}
}참고
'Computer Science > Algorithm' 카테고리의 다른 글
| [알고리즘] BFS(넓이 우선 탐색) & DFS(깊이 우선 탐색) - javascript (0) | 2023.01.18 |
|---|---|
| [알고리즘] 정렬(버블, 삽입, 선택, 합병, 퀵, 기수) - javascript (0) | 2023.01.17 |
| [알고리즘] 재귀 문제 풀이 - javascript (0) | 2022.08.02 |
| [알고리즘] javascript 문제해결 패턴 - Sliding Window (기준점 간 이동) (0) | 2022.07.27 |
| [알고리즘] javascript 문제해결 패턴 - Multiple Pointers (다중 포인터) (0) | 2022.07.26 |