주어진 넓이를 주어진 타일로 채우라는 문제인 타일링은 다이나믹 프로그래밍의 기본 알고리즘이다.
타일링은 재귀적 사고방식으로 봐야 패턴을 확인 할 수 있다.
f(1), f(2), f(3) ... 같이 순차적으로 값을 파악하기보다
f(n), f(n-1), f(n-2) 같이 ... 역순으로 파악하며 구조와 패턴을 찾아야 한다는 것이다.
타일링의 패턴을 찾으려면 거쳐야 하는 과정을 다음과 같다.
맨 마지막에 들어갈 수 있는 타일의 경우의 수 찾기 -> 넓이가 증가할 때마다 나타나는 특이 케이스 찾기
가장 기본인 2xn 타일링부터 더 큰 넓이까지 차례대로 따라가보자.
(이해를 돕기 위해 그림을 그렸으나... 그림판 발그림이라는 것을 감안해주세요)
📌 2xn 타일링
2x1 크기의 직사각형 타일을 이용해 2xn 넓이를 채우는 경우의 수의 개수 구하기
구현 과정
2xn을 채우는 경우의 수 개수= f(n)
먼저 f(n)에서 맨 마지막에 오는 타일의 경우의 수를 따져보면 오직 두 가지 경우밖에 없다.
- 하나가 세워져 있음
- 두 개가 눕혀져 있음
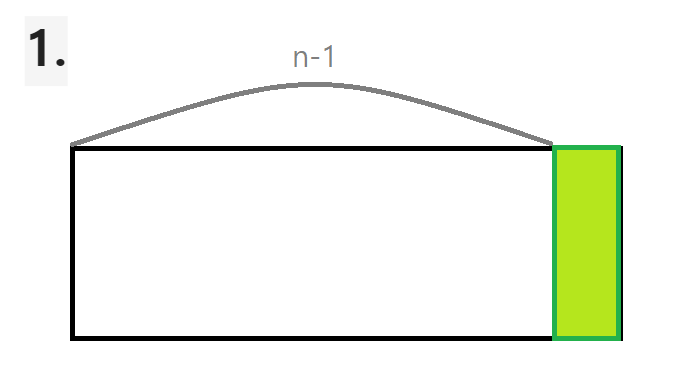
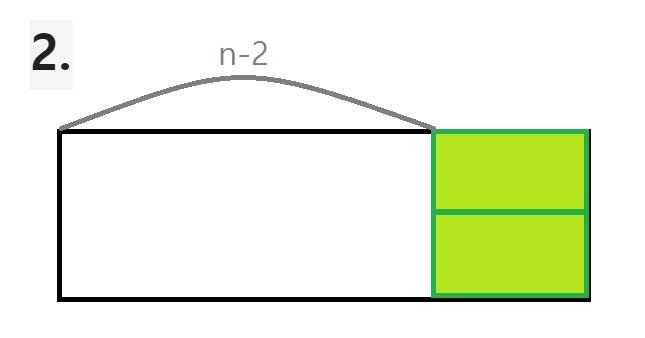
2번에서 타일 두 개를 세운 것도 다른 경우의 수 아닌가? 싶지만, 이 경우는 1번에 해당한다.
맨 마지막 타일이 세워져 있으니 1번 안에 이 경우도 포함인 것이다.
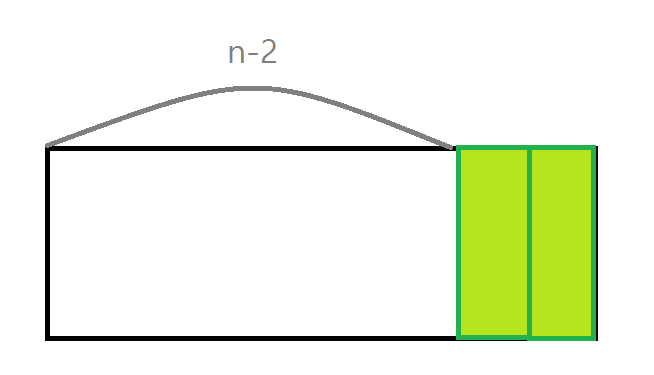
이런 패턴으로 보면 f(n)은 f(n-1)의 모든 경우의 수 + f(n-2)의 모든 경우의 수가 된다.
어차피 맨 뒤 타일은 고정되어 있기 때문에 그 앞의 경우의 수만 구하면 되기 때문이다.
최종 점화식
f(n) = f(n-1) + f(n-2)
피보나치의 수 공식과 같다.
* 초기값 설정 : f(0) = 1 / f(1) = 1 / f(2) = 2
(문제 풀이) [프로그래머스] 2xn 타일링 (Lv 2) - javascript
➕ 가능한 타일이 2x1 & 2x2 인 경우
맨 끝에 들어갈 수 있는 경우의 수는 아래와 같다.
- 2x1 세워서 한 개 => f(n-1)
- 2x1 눕혀서 두 개 => f(n-2)
- 2x2 한 개 => f(n-2)
* 최종 점화식
f(n) = f(n-1) + 2 * f(n-2)
* 초기값 설정 : f(1) = 1 / f(2) = 3
📌 3xn 타일링
1x2 타일로 3xn의 넓이를 채우는 경우의 수의 개수 구하기
구현 과정
먼저 2xn 타일링과 같이 맨 마지막에 오는 타일의 경우의 수부터 따져보자.
타일 하나만 세워놓는 것은 불가능하다. 밑에 1의 공간이 남기 때문이다.
결론적으로 최소 가로가 2는 되어야 채울 수 있고, 경우의 수 3가지가 나온다.
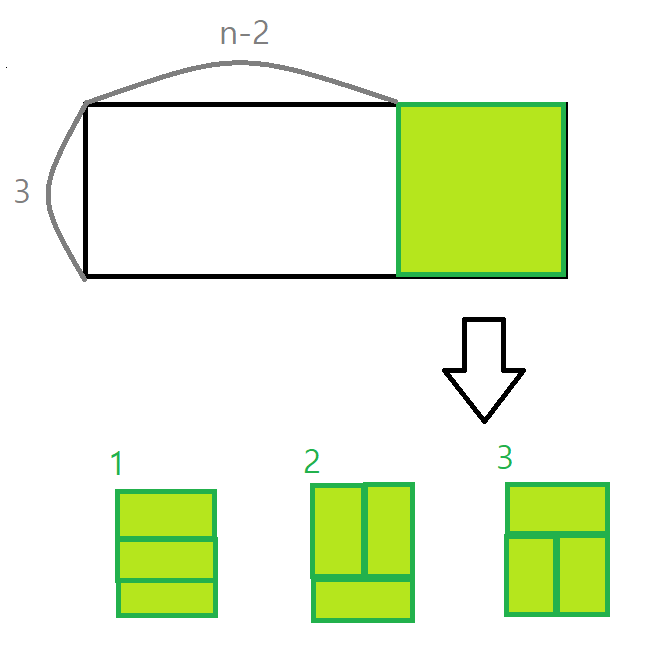
그런데 여기서 끝이 아니라, 4부터 2의 배수가 될 때마다 특이 케이스가 2개씩 생겨난다.
2와 2가 만날 때마다 또 그 사이에서 2가 생성되고 아래와 같이 타일을 넣을 수 있기 때문이다.
(머릿 속으로 이해한 다음, 공식을 외우는 것이 편하다)
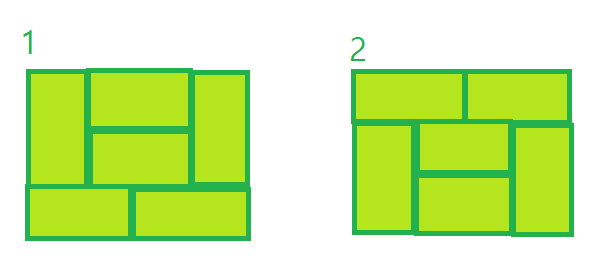
그러므로 f(n)은 f(n-2)의 경우의 수 x 3 에서 f(n-4)*2 + f(n-6)*2 + f(n-8)*2 ... 를 더한 값이다.
최종 점화식
f(n) = f(n-2) * 3 + (f(n-4) * 2 + f(n-6) * 2 ... f(0) * 2)
* 초기값 설정 : f(0) = 1 / f(1) = 0 / f(2) = 3
(문제 풀이) [프로그래머스] 3xn 타일링 (Lv 2) - javascript
📌 2xn을 더 작은 타일로 채우기
2xn 넓이를 2x1, 2x2, 1x1의 타일로 채우는 경우의 수 구하기
구현 과정
맨 끝에 타일을 놓는 경우의 수는 5가지다.
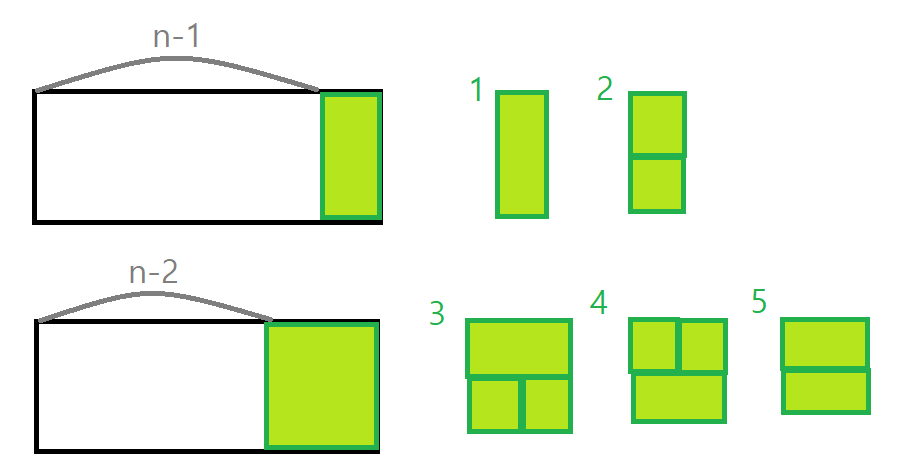
그리고 3씩 증가할 때마다 특이 케이스가 2개씩 나타난다.
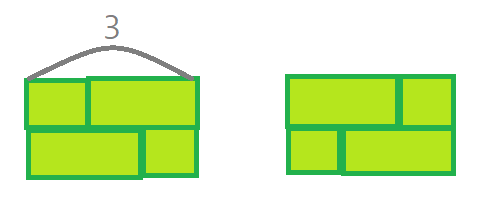
최종 점화식
f(n) = f(n-2) * 3 + f(n-1) * 2 + (f(n-3) * 2 + f(n-6) * 2 ... f(0) * 2)
* 초기값 설정 : f(0) = 1 / f(1) = 2 / f(2) = 7
🔑 구현 시, 유의사항
1. 재귀로 풀면 스택오버플로우가 날 확률이 높다.
다이나믹 프로그래밍으로 바텀탑으로 올라가며 풀어야 한다.
2. 피보나치 수이므로 수가 엄청나게 커지기 때문에 나머지 값을 반환하라는 문제가 많다.
[알고리즘] 피보나치 수 (다이나믹 프로그래밍) - javascript
참고
'Computer Science > Algorithm' 카테고리의 다른 글
| [알고리즘] javascript 문제해결 패턴 - frequency counter(빈도 카운터) (0) | 2022.07.26 |
|---|---|
| [알고리즘] 다이나믹 프로그래밍(동적 계획법) - javascript (0) | 2022.06.14 |
| [알고리즘] 하노이의 탑 - javascript (0) | 2022.06.10 |
| [알고리즘] 순열과 조합 - javascript (0) | 2022.05.07 |
| [알고리즘] 최대공약수와 최소공배수 - javascript (0) | 2022.04.16 |